最长的严格递增或递减子数组
给你一个整数数组 nums 。
返回数组 nums 中 严格递增 或 严格递减 的最长非空子数组的长度。
示例 1:
输入:nums = [1,4,3,3,2]
输出:2
解释:
nums 中严格递增的子数组有[1]、[2]、[3]、[3]、[4] 以及 [1,4] 。
nums 中严格递减的子数组有[1]、[2]、[3]、[3]、[4]、[3,2] 以及 [4,3] 。
因此,返回 2 。
示例 2:
输入:nums = [3,3,3,3]
输出:1
解释:
nums 中严格递增的子数组有 [3]、[3]、[3] 以及 [3] 。
nums 中严格递减的子数组有 [3]、[3]、[3] 以及 [3] 。
因此,返回 1 。
示例 3:
输入:nums = [3,2,1]
输出:3
解释:
nums 中严格递增的子数组有 [3]、[2] 以及 [1] 。
nums 中严格递减的子数组有 [3]、[2]、[1]、[3,2]、[2,1] 以及 [3,2,1] 。
因此,返回 3 。
正向跑一遍,可以构造一个数组枚举正向的递增最大长度在当前位,反向也跑一次,从而两个数组的最大值为答案
#define all(c) (c).begin(), (c).end()
class Solution {
public:
int longestMonotonicSubarray(vector<int> &nums) {
vector<int> f(nums.size(), 1);
for (int i = 1; i < nums.size(); i++) {
if (nums[i] > nums[i - 1]) {
f[i] = f[i - 1] + 1;
}
}
vector<int> f1(nums.size(), 1);
for (int i = 1; i < nums.size(); i++) {
if (nums[i] < nums[i - 1]) {
f1[i] = f1[i - 1] + 1;
}
}
return max(*max_element(all(f)), *max_element(all(f1)));
}
};给你一个字符串 s 和一个整数 k 。
定义函数 distance(s1, s2) ,用于衡量两个长度为 n 的字符串 s1 和 s2 之间的距离,即:
- 字符
'a'到'z'按 循环 顺序排列,对于区间[0, n - 1]中的i,计算所有「s1[i]和s2[i]之间 最小距离」的 和 。
例如,distance("ab", "cd") == 4 ,且 distance("a", "z") == 1 。
你可以对字符串 s 执行 任意次 操作。在每次操作中,可以将 s 中的一个字母 改变 为 任意 其他小写英文字母。
返回一个字符串,表示在执行一些操作后你可以得到的 字典序最小 的字符串 t ,且满足 distance(s, t) <= k 。
示例 1:
输入:s = "zbbz", k = 3
输出:"aaaz"
解释:在这个例子中,可以执行以下操作:
将 s[0] 改为 'a' ,s 变为 "abbz" 。
将 s[1] 改为 'a' ,s 变为 "aabz" 。
将 s[2] 改为 'a' ,s 变为 "aaaz" 。
"zbbz" 和 "aaaz" 之间的距离等于 k = 3 。
可以证明 "aaaz" 是在任意次操作后能够得到的字典序最小的字符串。
因此,答案是 "aaaz" 。示例 2:
输入:s = "xaxcd", k = 4
输出:"aawcd"
解释:在这个例子中,可以执行以下操作:
将 s[0] 改为 'a' ,s 变为 "aaxcd" 。
将 s[2] 改为 'w' ,s 变为 "aawcd" 。
"xaxcd" 和 "aawcd" 之间的距离等于 k = 4 。
可以证明 "aawcd" 是在任意次操作后能够得到的字典序最小的字符串。
因此,答案是 "aawcd" 。示例 3:
输入:s = "lol", k = 0
输出:"lol"
解释:在这个例子中,k = 0,更改任何字符都会使得距离大于 0 。
因此,答案是 "lol" 。提示:
1 <= s.length <= 1000 <= k <= 2000s只包含小写英文字母。
由于字符串长度不变,要使其字典变小,应该从第一位开始让其尽量变小,并且是越小越好,此时可以让前面的枚举其可在当前情况下变化的最小字符进行替换。
class Solution {
public:
int dis(char a, char b) {
return min(abs(b - a), 26 - abs(b - a));
}
string getSmallestString(string s, int k) {
int n = s.size();
for (int i = 0; i < n && k > 0; i++) {
for (char a = 'a'; a <= 'z'; a++) {
if (dis(a, s[i]) <= k) {
k -= dis(a, s[i]);
s[i] = a;
break;
}
}
}
return s;
}
};给你一个整数数组 nums 和一个 非负 整数 k 。一次操作中,你可以选择任一元素 加 1 或者减 1 。
请你返回将 nums 中位数 变为 k 所需要的 最少 操作次数。
一个数组的中位数指的是数组按非递减顺序排序后最中间的元素。如果数组长度为偶数,我们选择中间两个数的较大值为中位数。
示例 1:
输入:nums = [2,5,6,8,5], k = 4
输出:2
解释:我们将 nums[1] 和 nums[4] 减 1 得到 [2, 4, 6, 8, 4] 。现在数组的中位数等于 k 。
示例 2:
输入:nums = [2,5,6,8,5], k = 7
输出:3
解释:我们将 nums[1] 增加 1 两次,并且将 nums[2] 增加 1 一次,得到 [2, 7, 7, 8, 5] 。
示例 3:
输入:nums = [1,2,3,4,5,6], k = 4
输出:0
解释:数组中位数已经等于 k 了。
提示:
1 <= nums.length <= 2 * 1000001 <= nums[i] <= 100000000001 <= k <= 10000000000
对于一个数组,排序后中位数的位置按照定义可知应该为nums[n / 2];
排序后,nums[n/2]有三种情况
- nums[n/2] = k无需修改
- nums[n/2]<k 则意味着要把当前值改为k,那么前面可能还会有值比k大,需要把[0,n/2]的大于k的都修改为k,代价为 nums[i] - k
- nums[n/2]>k 则意味着要把当前值改为k,那么前面可能还会有值比k小,需要把[n/2,n]的大于k的都修改为k,代价为 nums[i] - k
class Solution {
public:
long long minOperationsToMakeMedianK(vector<int> &nums, int k) {
int n = nums.size();
sort(nums.begin(), nums.end());
int idx = n / 2;
long long ans = 0;
if (nums[idx] < k) {
for (int i = idx; i < n; i++) {
if (nums[i] < k) {
ans += k - nums[i];
}
}
} else {
for (int i = idx; i >= 0; --i) {
if (nums[i] > k) {
ans += nums[i] - k;
}
}
}
return ans;
}
};给你一个 n 个节点的带权无向图,节点编号为 0 到 n - 1 。
给你一个整数 n 和一个数组 edges ,其中 edges[i] = [ui, vi, wi] 表示节点 ui 和 vi 之间有一条权值为 wi 的无向边。
在图中,一趟旅途包含一系列节点和边。旅途开始和结束点都是图中的节点,且图中存在连接旅途中相邻节点的边。注意,一趟旅途可能访问同一条边或者同一个节点多次。
如果旅途开始于节点 u ,结束于节点 v ,我们定义这一趟旅途的 代价 是经过的边权按位与 AND 的结果。换句话说,如果经过的边对应的边权为 w0, w1, w2, ..., wk ,那么代价为w0 & w1 & w2 & ... & wk ,其中 & 表示按位与 AND 操作。
给你一个二维数组 query ,其中 query[i] = [si, ti] 。对于每一个查询,你需要找出从节点开始 si ,在节点 ti 处结束的旅途的最小代价。如果不存在这样的旅途,答案为 -1 。
返回数组 answer ,其中 answer[i] 表示对于查询 i 的 最小 旅途代价。
示例 1:
输入:n = 5, edges = [[0,1,7],[1,3,7],[1,2,1]], query = [[0,3],[3,4]]
输出:[1,-1]
解释:
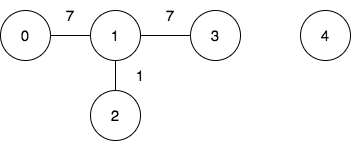
第一个查询想要得到代价为 1 的旅途,我们依次访问:0->1(边权为 7 )1->2 (边权为 1 )2->1(边权为 1 )1->3 (边权为 7 )。
第二个查询中,无法从节点 3 到节点 4 ,所以答案为 -1 。
示例 2:
输入:n = 3, edges = [[0,2,7],[0,1,15],[1,2,6],[1,2,1]], query = [[1,2]]
输出:[0]
解释:
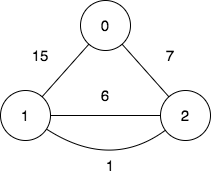
第一个查询想要得到代价为 0 的旅途,我们依次访问:1->2(边权为 1 ),2->1(边权 为 6 ),1->2(边权为 1 )。
提示:
1 <= n <= 1050 <= edges.length <= 105edges[i].length == 30 <= ui, vi <= n - 1ui != vi0 <= wi <= 1051 <= query.length <= 105query[i].length == 20 <= si, ti <= n - 1
这个题首先要知道,选中的边越多,&运算的值越多,则&的结果越小
在同一个连同块内,可以直接把所有边都选中,并把值AND到一起,结果就是这个连通块内任意两点的代价
不在一个连通块内则为-1,同起点终点为0
用并查集维护连通块,并且同时还可以维护这个连通块的代价,查询时直接判定并取值即可
class Solution {
public:
vector<int> minimumCost(int n, vector<vector<int>> &edges, vector<vector<int>> &queries) {
vector<int> f(n), t(n, INT_MAX), ans;
iota(f.begin(), f.end(), 0);
function<int(int)> find = [&](int x){
return f[x] == x ? x : f[x] = find(f[x]);
};
for(vector<int> & e: edges){
int u = find(e[0]), v = find(e[1]), w = e[2];
if(u == v) t[u] &= w;
else t[min(u, v)] &= t[max(u,v)] & w, f[max(u, v)] = min(u, v);
}
for(vector<int> & q : queries){
int s = find(q[0]), e = find(q[1]);
if(q[0] == q[1]) ans.push_back(0);
else if(s == e) ans.push_back(t[s]);
else ans.push_back(-1);
}
return ans;
}
};








Comments | NOTHING