Decode the Message3

You are given the strings key and message, which represent a cipher key and a secret message, respectively. The steps to decode message are as follows:

1. Use the first appearance of all 26 lowercase English letters in key as the order of the substitution table.
2. Align the substitution table with the regular English alphabet.
3. Each letter in message is then substituted using the table.
4. Spaces ' ' are transformed to themselves.

• For example, given key = "happy boy" (actual key would have at least one instance of each letter in the alphabet), we have the partial substitution table of ('h' -> 'a', 'a' -> 'b', 'p' -> 'c', 'y' -> 'd', 'b' -> 'e', 'o' -> 'f').

Return the decoded message.

Example 1:

Input: key = "the quick brown fox jumps over the lazy dog", message = "vkbs bs t suepuv"
Output: "this is a secret"
Explanation: The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "the quick brown fox jumps over the lazy dog".

模拟呗，就是按照key去生成个字典，然后给message还原了，没啥坑，注意一下顺序就行。

#include<bits/stdc++.h>

using namespace std;
class Solution {
public:
string decodeMessage(string key, string message) {
map<char, char> k;
char ch = 'a';
for (auto &c: key) {
if (c != ' ' && !k.count(c)) {
k[c] = ch;
ch++;
}
}
for (auto &i: message) {
if (i != ' ') {
i = k[i];
}
}
return message;
}
};
signed main() {
Solution s;
cout << s.decodeMessage("the quick brown fox jumps over the lazy dog", "vkbs bs t suepuv");
}

Spiral Matrix IV

You are given two integers m and n, which represent the dimensions of a matrix.

You are also given the head of a linked list of integers.

Generate an m x n matrix that contains the integers in the linked list presented in spiral order (clockwise), starting from the top-left of the matrix. If there are remaining empty spaces, fill them with -1.

Return the generated matrix.

Example 1:

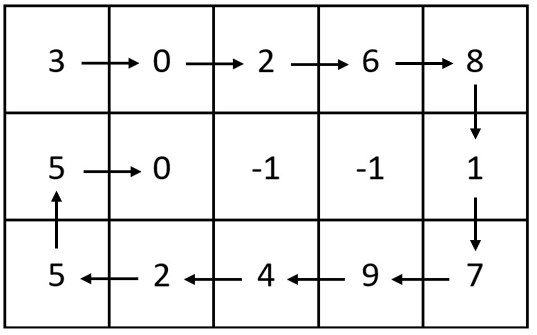
Input: m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
Output: [[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]
Explanation: The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.

老题了，原题自动机，生成个vector,然后去生成螺旋。

偷板子就偷！这玩意多块

/**


Definition for singly-linked list.
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}

};
/
class Solution {
private:
static constexpr int directions[4][2] = {{0,  1},
{1,  0},
{0,  -1},
{-1, 0}};
public:
vector<vector<int>> spiralMatrix(int m, int n, ListNode head) {
vector<int> val;
vector<vector<int>> ans(m, vector<int>(n));
while (head != NULL) {
val.push_back(head->val);
head = head->next;
}
while (n  m > val.size()) {
val.push_back(-1);
}
int rows = ans.size(), columns = ans[0].size();
vector<vector<bool>> visited(rows, vector<bool>(columns));
int total = rows  columns;
vector<int> order(total);
int row = 0, column = 0;
int directionIndex = 0;
for (int i = 0; i < total; i++) {
    ans[row][column] = val[i];
    visited[row][column] = true;
    int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
    if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns ||
        visited[nextRow][nextColumn]) {
        directionIndex = (directionIndex + 1) % 4;
    }
    row += directions[directionIndex][0];
    column += directions[directionIndex][1];
}
return ans;
}
 };
Number of People Aware of a Secret
2327. Number of People Aware of a Secret
On day 1, one person discovers a secret.
You are given an integer delay, which means that each person will share the secret with a new person every day, starting from delay days after discovering the secret. You are also given an integer forget, which means that each person will forget the secret forget days after discovering it. A person cannot share the secret on the same day they forgot it, or on any day afterwards.
Given an integer n, return the number of people who know the secret at the end of day n. Since the answer may be very large, return it modulo 109 + 7.
Example 1:
Input: n = 6, delay = 2, forget = 4
Output: 5
Explanation:
Day 1: Suppose the first person is named A. (1 person)
Day 2: A is the only person who knows the secret. (1 person)
Day 3: A shares the secret with a new person, B. (2 people)
Day 4: A shares the secret with a new person, C. (3 people)
Day 5: A forgets the secret, and B shares the secret with a new person, D. (3 people)
Day 6: B shares the secret with E, and C shares the secret with F. (5 people)
一眼dp
打个表把，记不住
1
2
3
4
5
6
1
0
1
1
1
2
0
0
0
0
1
0
1
0
1
1
0
2
$dp[i][0]=\sum_{i-forget+1}^{i-delay}$
$dp[i][1]=dp[i-forget][0]$
转移求和，看到10**9+7，上py！
#include<bits/stdc++.h>

using namespace std;
class Solution {
public:
int peopleAwareOfSecret(int n, int delay, int forget) {
vector<vector<int64_t>> dp(n + 1, vector<int64_t>(2, 0));
dp[1][0] = 1;
for (int i = i + delay; i <= n; i++) {
for (int j = max(0, i - forget) + 1; j <= i - delay; j++) {
dp[i][0] += dp[j][0];
dp[i][0] %= 1000000007;
}
if (i - forget >= 1) {
dp[i][1] = dp[i - forget][0];
dp[i][1] %= 1000000007;
}
}
int64_t ans = 0;
for (int i = 1; i <= n; i++) {
ans += dp[i][0] - dp[i][1];
}
return ans % 1000000007;
}
};
signed main() {
Solution s;
cout << s.peopleAwareOfSecret(6, 2, 4);
}
Number of Increasing Paths in a Grid
You are given an m x n integer matrix grid, where you can move from a cell to any adjacent cell in all 4 directions.
Return the number of strictly increasing paths in the grid such that you can start from any cell and end at any cell. Since the answer may be very large, return it modulo 109 + 7.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
Example 1:
 
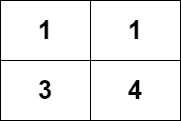
Input: grid = [[1,1],[3,4]]
Output: 8
Explanation: The strictly increasing paths are:


Paths with length 1: [1], [1], [3], [4].
Paths with length 2: [1 -> 3], [1 -> 4], [3 -> 4].
Paths with length 3: [1 -> 3 -> 4].
The total number of paths is 4 + 3 + 1 = 8.
所有能递增的子序列，记忆化每个点，然后求和？
原题把，哈哈哈哈哈哈哈哈哈哈哈，
总结，今天原题自动机的一天
class Solution:

    DIRS = [(-1, 0), (1, 0), (0, -1), (0, 1)]

    def countPaths(self, matrix: List[List[int]]) -> int:
        if not matrix:
            return 0

        @lru_cache(None)
        def dfs(row: int, column: int) -> int:
            best = 1
            for dx, dy in Solution.DIRS:
                newRow, newColumn = row + dx, column + dy
                if 0 <= newRow < rows and 0 <= newColumn < columns and matrix[newRow][newColumn] > matrix[row][column]:
                    best += dfs(newRow, newColumn)
            return best

        ans = 0
        rows, columns = len(matrix), len(matrix[0])
        for i in range(rows):
            for j in range(columns):
                ans += dfs(i, j)
                ans%=10**9+7
        return ans