Check if Matrix Is X-Matrix

A square matrix is said to be an X-Matrix if both of the following conditions hold:

1. All the elements in the diagonals of the matrix are non-zero.
2. All other elements are 0.

Given a 2D integer array grid of size n x n representing a square matrix, return true if grid is an X-Matrix. Otherwise, return false.

Example 1:

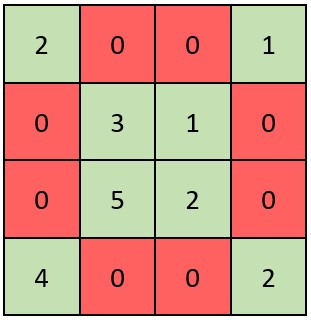
Input: grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
Output: true
Explanation: Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.

对角线都是0，不是对角线都不是0；扫他妈的，日常脑抽

class Solution {
public:
bool checkXMatrix(vector<vector<int>>& grid) {
for(int i = 0 ;i<grid.size();i++){
for(int j =0 ;j<grid.size();j++){
if(grid[i][j]!=0){
if(!(i==j||j==grid.size()-1-i)){
return false;
}
}
if((i==j||j==grid.size()-1-i)){
if(grid[i][j]==0)
return false;
}
}
}
return true;
}
};

Count Number of Ways to Place Houses

There is a street with n * 2 plots, where there are n plots on each side of the street. The plots on each side are numbered from 1 to n. On each plot, a house can be placed.

Return the number of ways houses can be placed such that no two houses are adjacent to each other on the same side of the street. Since the answer may be very large, return it modulo 109 + 7.

Note that if a house is placed on the ith plot on one side of the street, a house can also be placed on the ith plot on the other side of the street.

Example 2:

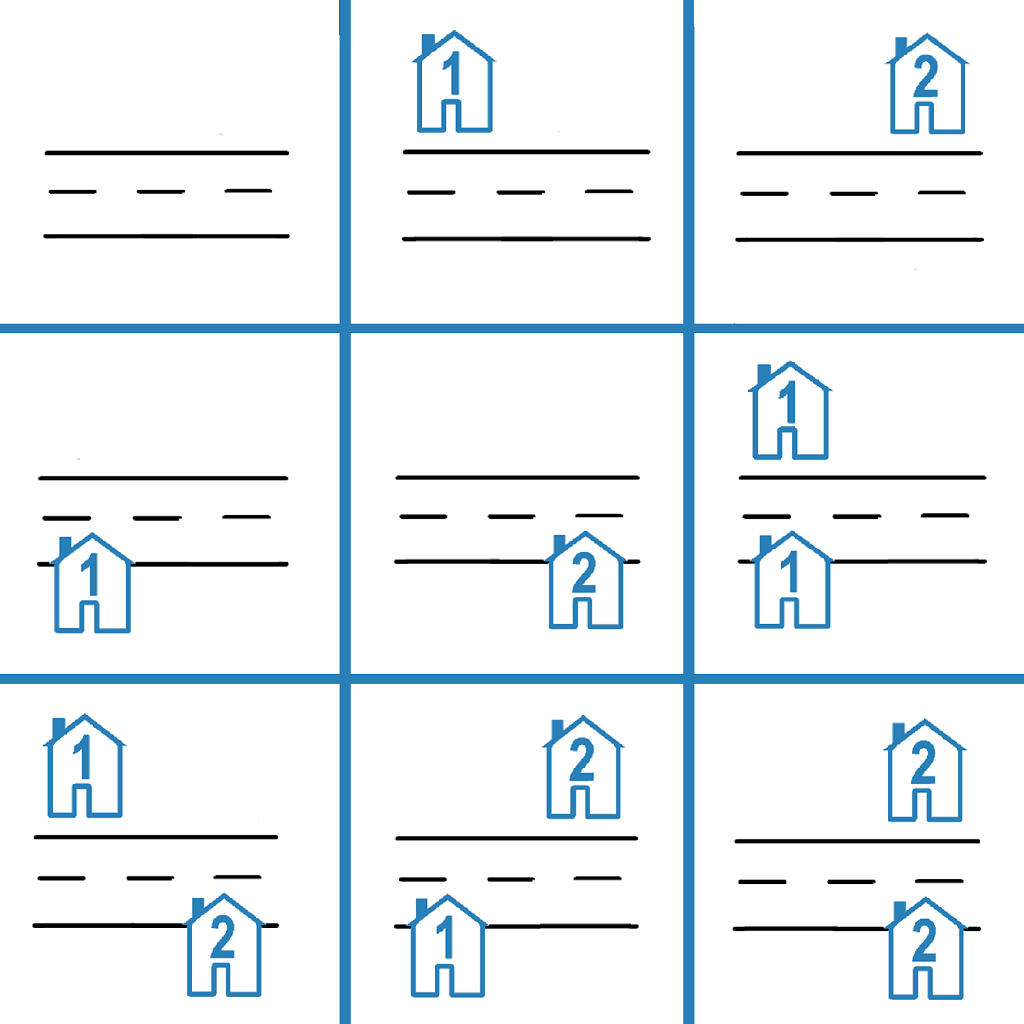
Input: n = 2
Output: 9
Explanation: The 9 possible arrangements are shown in the diagram above.

$$dp[0][0]=1$$

$$dp[0][1]=1$$

$$dp[i][0]=dp[i-1][1]$$

$$dp[i][1]=dp[i-1][0]+dp[i-1][1]$$

应该对，试试！！

啊啊啊啊啊我是傻逼，我咋还能。。。少个0

class Solution:
def countHousePlacements(self, n: int) -> int:
a,b=1,1
for i in range(1,n):
a,b=a+b,a
return (a+b)**2%1000000007

Maximum Score Of Spliced Array

You are given two 0-indexed integer arrays nums1 and nums2, both of length n.

You can choose two integers left and right where 0 <= left <= right < n and swap the subarray nums1[left...right] with the subarray nums2[left...right].

• For example, if nums1 = [1,2,3,4,5] and nums2 = [11,12,13,14,15] and you choose left = 1 and right = 2, nums1 becomes [1,12,13,4,5] and nums2 becomes [11,2,3,14,15].

You may choose to apply the mentioned operation once or not do anything.

The score of the arrays is the maximum of sum(nums1) and sum(nums2), where sum(arr) is the sum of all the elements in the array arr.

Return the maximum possible score.

A subarray is a contiguous sequence of elements within an array. arr[left...right] denotes the subarray that contains the elements of nums between indices left and right (inclusive).

Example 1:

Input: nums1 = [60,60,60], nums2 = [10,90,10]
Output: 210
Explanation: Choosing left = 1 and right = 1, we have nums1 = [60,90,60] and nums2 = [10,60,10].
The score is max(sum(nums1), sum(nums2)) = max(210, 80) = 210.

交换一段区间，让交换后其中一个数组最大。

$$Nsum1=sum1-\sum_{n=l}^{r}(nums2[n]-nums1[n])$$

$$Nsum2=sum2-\sum_{n=l}^{r}(nums1[n]-nums2[n])$$

肯定要做差了，然后取个最长。懒人透板子

class Solution {
public:
int maxSubArray(vector<int>& nums) {
int pre = 0, maxAns = nums[0];
for (const auto &x: nums) {
pre = max(pre + x, x);
maxAns = max(maxAns, pre);
}
return maxAns;
}
int maximumsSplicedArray(vector<int>& nums1, vector<int>& nums2) {
vector<int> c(nums1.size());
vector<int> cc(nums1.size());
int sum1=0;
int sum2=0;
for(int i =0 ;i<nums1.size();i++){
c[i]=nums1[i]-nums2[i];
cc[i]=-c[i];
sum1+=nums1[i];
sum2+=nums2[i];
}
return max(sum1+maxSubArray(cc),sum2+maxSubArray(c));

}
};
Minimum Score After Removals on a Tree
There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.
You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the ith node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
Remove two distinct edges of the tree to form three connected components. For a pair of removed edges, the following steps are defined:
Get the XOR of all the values of the nodes for each of the three components respectively.
The difference between the largest XOR value and the smallest XOR value is the score of the pair.
For example, say the three components have the node values: [4,5,7], [1,9], and [3,3,3]. The three XOR values are 4 ^ 5 ^ 7 = 6, 1 ^ 9 = 8, and 3 ^ 3 ^ 3 = 3. The largest XOR value is 8 and the smallest XOR value is 3. The score is then 8 - 3 = 5.
Return the minimum score of any possible pair of edge removals on the given tree.
Example 1:
 
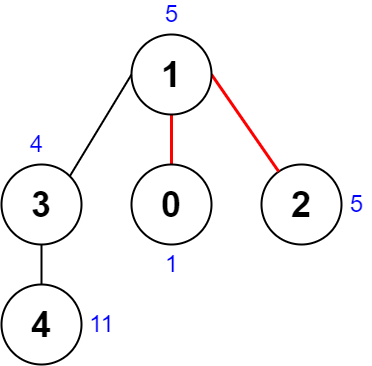
Input: nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
Output: 9
Explanation: The diagram above shows a way to make a pair of removals.


The 1st component has nodes [1,3,4] with values [5,4,11]. Its XOR value is 5 ^ 4 ^ 11 = 10.
The 2nd component has node [0] with value [1]. Its XOR value is 1 = 1.
The 3rd component has node [2] with value [5]. Its XOR value is 5 = 5.
The score is the difference between the largest and smallest XOR value which is 10 - 1 = 9.
It can be shown that no other pair of removals will obtain a smaller score than 9.
不想读，太长，
把树分成3个子部分，看每部分的xor和的最大和最小的差的最小值。DFS上
dfs遍历一下树的xor用性质后面用
然后给个时间戳判断父子关机
枚举每个点（0不能切割）
然后三种情况讨论一下
#include<bits/stdc++.h>

using namespace std;

class Solution {
public:
    int in[1001], o[1001], x[1001];
    vector<vector<int>> g;
    int t = 0;
    vector<int> nums;

    void dfs(int n, int f) {
        in[n] = ++t;
        x[n] = nums[n];
        for (auto &y: g[n]) {
            if (y == f) { continue; }
            dfs(y, n);
            x[n] = x[n] ^ x[y];
        }
        o[n] = t;
    }

    bool isP(int x, int y) { return in[x] <= in[y] && in[y] <= o[x]; }

    int minimumScore(vector<int> &nums, vector<vector<int>> &edges) {
        this->nums = nums;
        g = vector<vector<int>>(nums.size());
        for (auto &e: edges) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        dfs(0, -1);
        int ans = 0x3f3f3f3f;
        for (int i = 1; i < nums.size(); i++) {
            for (int j = 1; j < i; j++) {
                int a, b, c;
                if (isP(i, j)) { a = x[j], b = x[i] ^ x[j], c = x[0] ^ x[i]; }
                else if (isP(j, i)) { a = x[i], b = x[j] ^ x[i], c = x[0] ^ x[j]; }
                else { a = x[i], b = x[j], c = x[0] ^ a ^ b; }
                ans = min(ans, max({a, b, c}) - min({a, b, c}));
            }
        }
        return ans;
    }

};

signed main() {
    Solution s;
    vector<int> m = {1};
    vector<vector<int>> mm = {{1}};
    return 0;
}