一、引言
抽样是模拟信号数字化的过程,可以用于解决计算机无法处理储存模拟信号的问题。在时域采样定理的讲解过程中,对抽样函数对采样关联值的关系仍存在部分疑惑,对于为何 是理想抽样函数存在疑惑。通过课件中的静态图展示出了宽度会产生误差,但是不能体现出定量变化关系;在通过调制器进行乘积运算后得到的调制函数 随着抽样函数宽度和抽样函数形状的变化而发生的变化关系产生的定量变化关系。因此考虑使用模拟动画的方式进行变化过程的仿真观察及不同抽样函数的采样情况关系图。
通过分析零阶采样(逼近 函数)和一阶采样函数的关系,逐帧动态计算,从而得到调制函数和得到的采样点周围的一段模拟信号的数字信号的关联值。最后将帧合并得到抽样函数宽度变化对采样误差的影响关系。
二、时域采样定理
2.1 调制过程
抽样的一般结构模型中,第一步将被采样的模拟信号通过调制器(实质是一个乘法器),从而将调制信号和采样函数脉冲串进行乘积,从而得到采样点周围一段模拟信号。过程可以用如下式(1)表示。
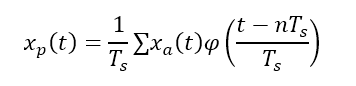
注:其中 是抽样后得到的一段模拟信号,由于采样函数是单位脉冲信号,因此得到的调制信号也是不连续的不规则脉冲串。
以形似随机生成的模拟信号 和零阶采样函数(宽度为2)为例,得到波形如下。红色的区域轮廓即可认为是调制函数的函数值。
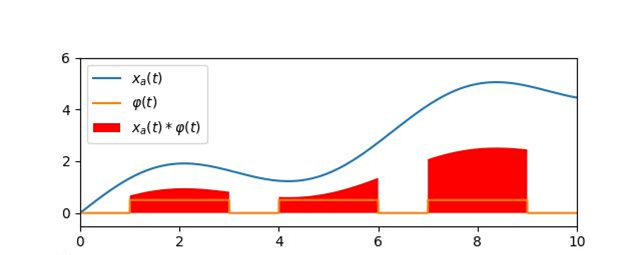
图1 调制过程示例
通过抽样的过程,并不能直接的观察到采样函数和采样值的直接关系。
2.2 模数转换过程
一般采样模型的第二步是将采样点周围的一段连续函数进行积分,得到模拟信号与数字信号的关联值。过程可以用如下公式(2)表示
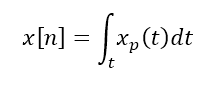
其意义在于将一段模拟信号进行转换,每个采样点调制后得到的不规则的脉冲串的积分面积作为这一点采样的结果。
但由于调制信号的长度关系,在这一点的积分并不是呈现线性相关关系的。同样以本节第一部分提到的两组信号为例,使用的是宽度为2,高度为 的采样函数,可以很容的发现每个调制信号的高度是原模拟信号的一半。而左右两部分并不是呈对称,且互相补充可以使得调制信号的积分面积是宽度为2,高度为采样值的一半的矩形。因此存在误差。
2.3 采样函数的分类
本次仿真中使用的采样函数有两类,零阶采样函数和一阶采样函数,零阶采样函数的关键点在于信号的宽度和高度,对于采样函数,应该保证每个脉冲的面积为1,因此其宽度和高度的乘积应该为1。
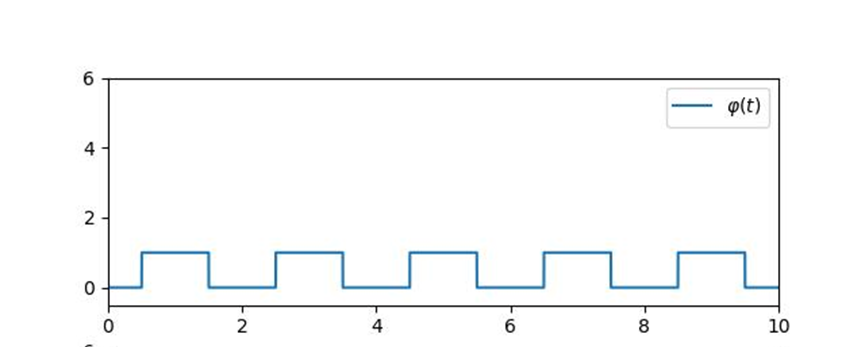
图2 零阶抽样函数示例
以宽度为1的零阶采样函数为例,则其高度应该也为1,以采样间隔 为2来绘制得到如图所示的采样函数。简单的写可以为一个如下式(3)的分段函数,在采样周期左右0.5的部分值为1,其余为0。
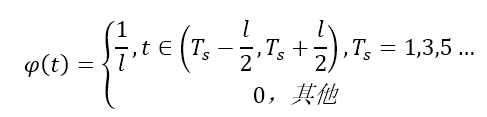
注:l是零阶采样函数的宽度
对于一阶采样函数,其实质的三角形函数,同样根据前面的分析,要保证其面积为1,因此同样假设脉冲宽度为l,高度为h,根据三角形面积公式 ,从而容易到l和r的关系如下式(4)。
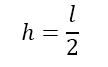
根据关系即可写出其分段函数如下式(5)。
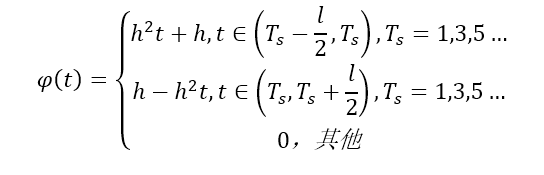
三、计算机实现
3.1 模拟信号生成和存储
由于计算机中储存的数据为离散的数字序列,因此直接生成模拟信号可行性较差,但是我们可以降低区间颗粒度,在生成横轴序列的过程中通过降低步长,从而实现序列间距变小,降低信号颗粒度的效果。
对于信号的序列产生,通过横轴坐标序列,带入到lambda公式中即可实现反馈纵坐标序列。在python中这些工作都可以通过科学计算库numpy进行简易的实现。在本次实验中,我们以10000Hz为信号采样长度,生成如 的信号。
3.2 调制过程实现
为了提高计算效率,降低时间复杂度到线性,在验证的过程中每次只考虑采样点 处的值。这样同时也简化了采样函数的生成,只需要通过区间进行判定和对应的值进行区间限制乘积即可得到抽样函数的序列表达式。
对于乘积过程,由于采样函数序列和模拟信号序列均采用了相同的时间间隔序列,因此可以直接进行按点相乘即可实现。
3.3 模数转换
根据前序的乘积函数,只需要对对应的区间进行卷积计算即可得知其积分,因此会定义一个借助用于积分的函数
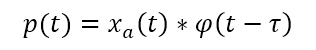
通过Scipy库的求和函数,即可得到这一点的积分值,即这一点的采样值。
3.4 图像生成
Python的图像生成与matlab相似,即将横纵坐标序列进行plot生成,并对标签进行修饰,为了方便查看,仿真实验中我们是将模拟信号、采样函数和乘积的区间面积进行了共同绘制。为了便于比较,同时还在第二绘图区将采样结果数值点在原信号区间内进行了放大查看。
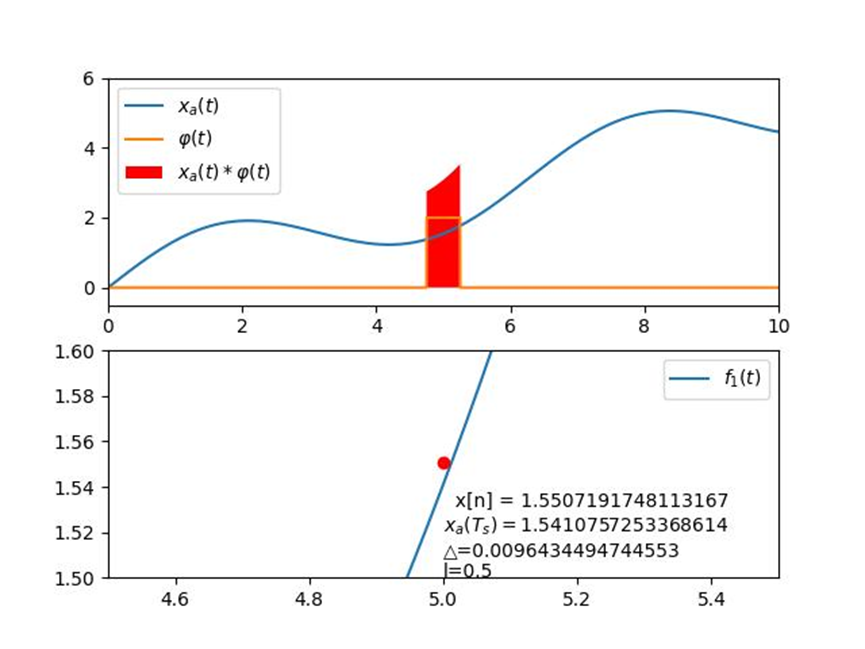
图3 零阶抽样结果示例(l=0.5,Ts=5)
3.5 动画生成
在matplotlib库中可以通过动态控制输入输出的交互关系来实现动态的绘制,只需要将前序的图像绘制过程进行封装,将其抽样信号的宽度作为变量即可完成相应点的帧图像绘制。
将每帧的图像转换成动画过程,可以通过imageio库进行实现,通过其中的gif生成功能,从而实现动画效果的采样函数函数展示。
3.6 交互界面
在python中可以用QT库实现快速的界面开发工作,其中函数数学表达式的控制,动画步长,采样函数都可以通过QT库实现调试。但由于时间问题,本部分工作并没有完全的完成。
四、仿真结果展示
五、结果分析
5.1 采样误差函数分析
在绘制动画过程中,由于已经进行了误差的计算,因此同时将(长度l,损失误差loss)元组进行的图像拟合,对于零阶采样函数,整体误差变化趋势如下图。
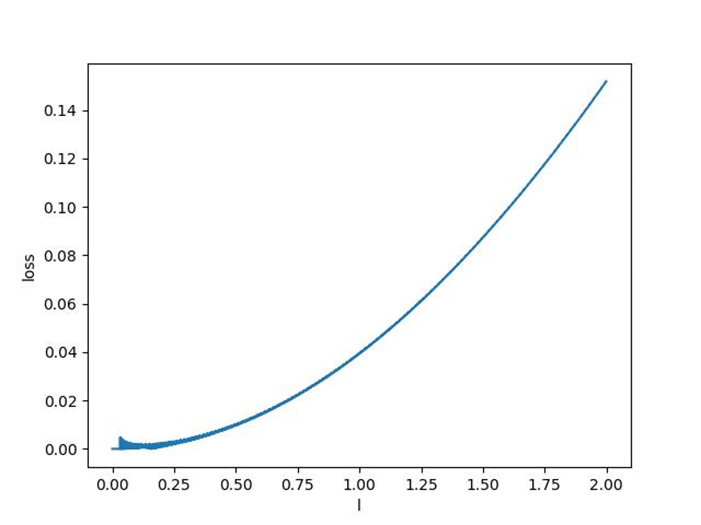
图4 零阶抽样误差随采样宽度变化关系图
对于零阶采样,在函数宽度较小的时候其误差整体较小,在0附近波动,通过改变采样点位置发现采样信号此时受到不同采样点的位置影响较为明显。
对于一阶采样函数,整体误差随函数宽度变化趋势如下图
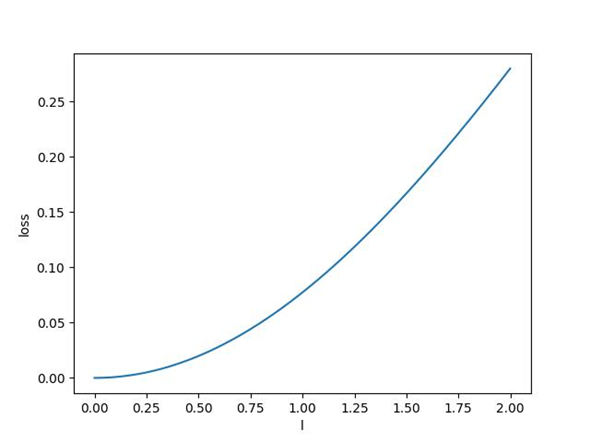
图5 一阶抽样误差随采样宽度变化关系图
对于一阶采样,同样在函数宽度较小的时候其误差整体较小,通过改变采样点位置发现采样信号此时受到不同采样点的位置影响较为明显。
5.2 两类采样函数误差对比
将组数据的曲线绘制在同一个图像中,发现在信号宽度较小时,一阶采样的误差整体较小,在抽样函数宽度较大时,零阶采样的误差整体较小。
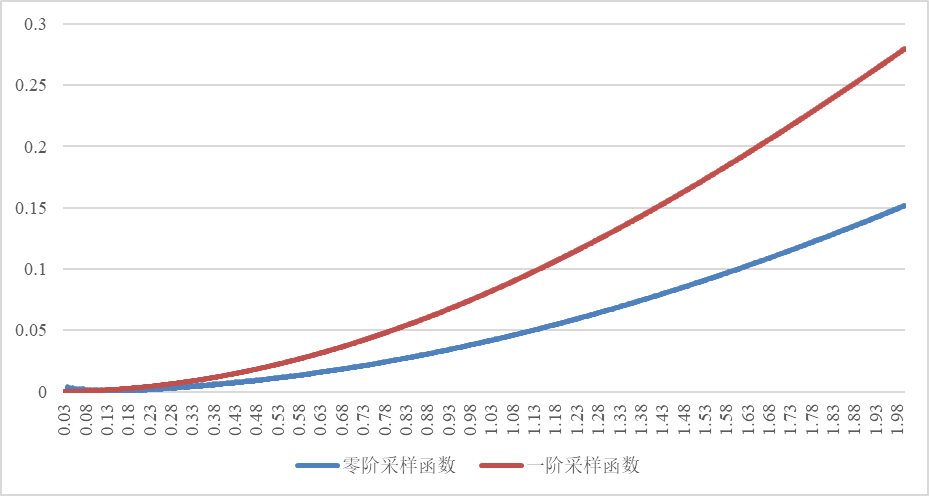
图6 零阶一阶采样误差对比图
5.3 采样点信号的影响
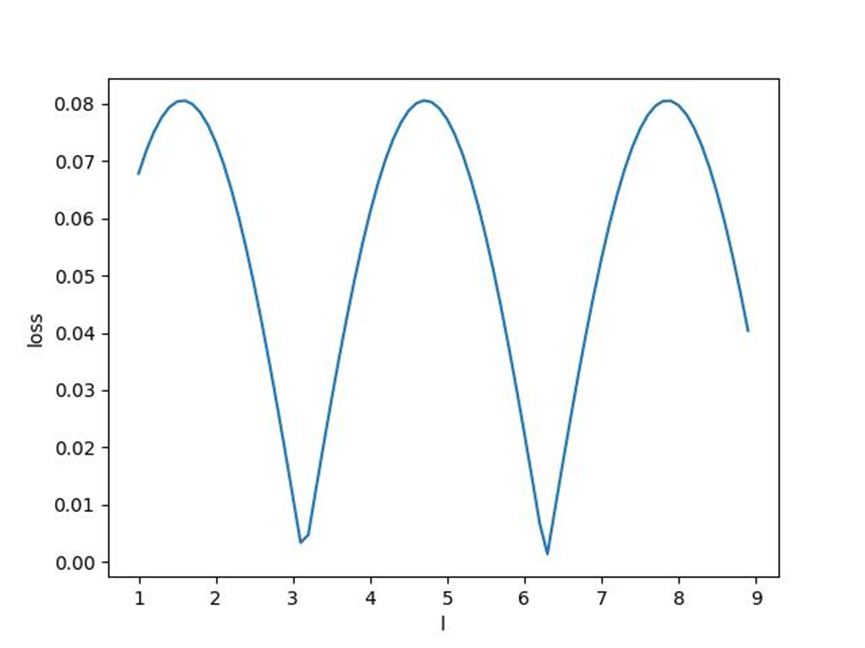
通过切换采样点,发现整体误差走势变化不大,均为随着采样函数宽度变大而发生的采样误差逐渐变大的趋势。最终不会收敛于一点。
六、总结
仿真过程通过python实现了在不同的采样点处,在计算机中通过零阶采样函数、一阶采样函数进行简化实现,并通过宽度变化的采样值关系动画模拟,从整体误差变化过程出发,得到了零阶和一阶采样函数在整体上的采样误差和采样函数宽度之间的变化关系都具有在0附近小幅度波动,然后误差逐渐增大的趋势。接下来通过对比分析两种采样函数的误差情况,发现在函数宽度较小的情况下,一阶采样信号的采样效果更号,在宽度较大的时候,零阶采样信号的效果更好。最后通过将每帧的绘制函数进行封装,并计划通过可视化交互框架实现更多的抽样函数,不同的采样点、步长参数进行模拟实现,从而通过动画演示实现更好的学习和教学的效果









Comments | NOTHING