A. Codeforces Checking
Given a lowercase Latin character (letter), check if it appears in the string codeforcescodeforces.
Input
The first line of the input contains an integer $t(1≤t≤26)$ — the number of test cases.
The only line of each test case contains a character $c$ — a single lowercase Latin character (letter).
Output
For each test case, output "YES" (without quotes) if $c$ satisfies the condition, and "NO" (without quotes) otherwise.
You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).
// A. Codeforces Checking
#include<bits/stdc++.h>
using namespace std;
#define all(c) (c).begin(), (c).end()
#define rev(a) reverse((a).begin(), (a).end())
#define each(x, a) for(auto& x : a)
#define mst(a, x) memset(a, x, sizeof(a))
#define rep(i, from, to) for(int i = from;i<to;i++)
#define rrep(i, from, to) for(i128 i = from;i>=to;i--)
#define to_uni(a) a.erase(unique(begin(a), end(a)), end(a))
#define fi first
#define se second
#define idx make_pair
#define pb push_back
#define endl "\n"
#define i128 __int128
#define ll long long
typedef pair<int, int> pii;
const int mod = 1e9 + 7;
const int dx[4]{1, 0, -1, 0}, dy[4]{0, 1, 0, -1};
const int fx[8] = {-1, -1, 0, 1, 1, 1, 0, -1}, fy[8] = {0, 1, 1, 1, 0, -1, -1, -1};
const int N = 1e5 + 10;
void solve() {
char ch;
cin >> ch;
string s = "codeforces";
if (s.find(ch) != s.npos) {
cout << "YES\n";
} else {
cout << "NO\n";
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}B. Following Directions
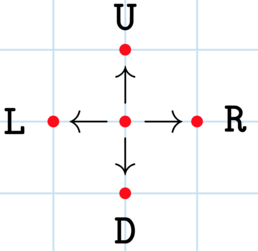
Alperen is standing at the point (0,0)(0,0). He is given a string s of length n and performs n moves. The i-th move is as follows:
- if si=L then move one unit left;
- if si=R, then move one unit right;
- if si=U, then move one unit up;
- if si=D, then move one unit down.
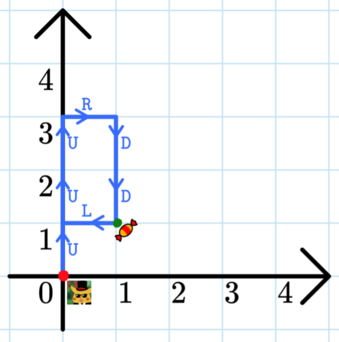
There is a candy at (1,1)(1,1) (that is, one unit above and one unit to the right of Alperen's starting point). You need to determine if Alperen ever passes the candy.
Input
The first line of the input contains an integer t (1≤t≤1000) — the number of testcases.
The first line of each test case contains an integer n (1≤n≤50) — the length of the string.
The second line of each test case contains a string s of length nconsisting of characters L, R, D, and U, denoting the moves Alperen makes.
Output
For each test case, output "YES" (without quotes) if Alperen passes the candy, and "NO" (without quotes) otherwise.
You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).
// B. Following Directions
#include<bits/stdc++.h>
using namespace std;
#define all(c) (c).begin(), (c).end()
#define rev(a) reverse((a).begin(), (a).end())
#define each(x, a) for(auto& x : a)
#define mst(a, x) memset(a, x, sizeof(a))
#define rep(i, from, to) for(int i = from;i<to;i++)
#define rrep(i, from, to) for(i128 i = from;i>=to;i--)
#define to_uni(a) a.erase(unique(begin(a), end(a)), end(a))
#define fi first
#define se second
#define idx make_pair
#define pb push_back
#define endl "\n"
#define i128 __int128
#define ll long long
typedef pair<int, int> pii;
const int mod = 1e9 + 7;
const int dx[4]{1, 0, -1, 0}, dy[4]{0, 1, 0, -1};
const int fx[8] = {-1, -1, 0, 1, 1, 1, 0, -1}, fy[8] = {0, 1, 1, 1, 0, -1, -1, -1};
const int N = 1e5 + 10;
void solve() {
int n;
cin >> n;
string s;
cin >> s;
int x = 0, y = 0;
for (auto &ch: s) {
if (ch == 'U')y++;
if (ch == 'R')x++;
if (ch == 'L')x--;
if (ch == 'D')y--;
if (x == 1 && y == 1) {
cout << "YES\n";
return;
}
// cerr << x << "," << y << endl;
}
cout << "NO\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}C. Prepend and Append
Timur initially had a binary string s (possibly of length 0). He performed the following operation several (possibly zero) times:
- Add 0 to one end of the string and 11 to the other end of the string. For example, starting from the string 1011, you can obtain either 010111 or 110110.
You are given Timur's final string. What is the length of the shortest possible string he could have started with?
†† A binary string is a string (possibly the empty string) whose characters are either 00 or 11.
// C. Prepend and Append
#include<bits/stdc++.h>
using namespace std;
#define all(c) (c).begin(), (c).end()
#define rev(a) reverse((a).begin(), (a).end())
#define each(x, a) for(auto& x : a)
#define mst(a, x) memset(a, x, sizeof(a))
#define rep(i, from, to) for(int i = from;i<to;i++)
#define rrep(i, from, to) for(i128 i = from;i>=to;i--)
#define to_uni(a) a.erase(unique(begin(a), end(a)), end(a))
#define fi first
#define se second
#define idx make_pair
#define pb push_back
#define endl "\n"
#define i128 __int128
#define ll long long
typedef pair<int, int> pii;
const int mod = 1e9 + 7;
const int dx[4]{1, 0, -1, 0}, dy[4]{0, 1, 0, -1};
const int fx[8] = {-1, -1, 0, 1, 1, 1, 0, -1}, fy[8] = {0, 1, 1, 1, 0, -1, -1, -1};
const int N = 1e5 + 10;
void solve() {
int n;
cin >> n;
string s;
cin >> s;
deque<char> ch(all(s));
while (ch.front() != ch.back() && ch.size() >= 2) {
ch.pop_back();
ch.pop_front();
}
// each(c, ch) cout << c;
cout << (ch).size() << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
} D. Distinct Split
Let's denote the f(x) function for a string x as the number of distinct characters that the string contains. For example $f(abc)=3$, $f(bbbbb)=1$, and$ f(babacaba)=3$.
Given a string s, split it into two non-empty strings a and b such that f(a)+f(b) is the maximum possible. In other words, find the maximum possible value of $f(a)+f(b)$such that a+b=s(the concatenation of string a and string b is equal to string s).
// D. Distinct Split
#include <bits/stdc++.h>
using namespace std;
#define all(c) (c).begin(), (c).end()
#define rev(a) reverse((a).begin(), (a).end())
#define each(x, a) for(auto& x : a)
#define mst(a, x) memset(a, x, sizeof(a))
#define rep(i, from, to) for(int i = from;i<to;i++)
#define rrep(i, from, to) for(i128 i = from;i>=to;i--)
#define to_uni(a) a.erase(unique(begin(a), end(a)), end(a))
#define fi first
#define se second
#define idx make_pair
#define pb push_back
#define endl "\n"
#define i128 __int128
#define ll long long
typedef pair<int, int> pii;
const int mod = 1e9 + 7;
const int dx[4]{1, 0, -1, 0}, dy[4]{0, 1, 0, -1};
const int fx[8] = {-1, -1, 0, 1, 1, 1, 0, -1}, fy[8] = {0, 1, 1, 1, 0, -1, -1, -1};
const int N = 1e5 + 10;
void solve() {
int n;
string s;
cin >> n >> s;
int f[256], c[256];
mst(f, 0);
mst(c, 0);
int ans = 0;
each(ch, s) f[ch]++;
rep(i, -1, n) {
if (i >= 0) {
f[s[i]]--;
c[s[i]]++;
}
int grade = 0;
for (char ch = 'a'; ch <= 'z'; ch++) {
if (f[ch] != 0) grade++;
if (c[ch] != 0) grade++;
}
ans = max(ans, grade);
}
cout << ans << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}E. Negatives and Positives
Given an array a consisting of n elements, find the maximum possible sum the array can have after performing the following operation any number of times:
- Choose 22 adjacent elements and flip both of their signs. In other words choose an index i� such that 1≤i≤n−1 and assign ai=−ai and ai+1=−ai+1.
// E. Negatives and Positives
#include <bits/stdc++.h>
using namespace std;
#define all(c) (c).begin(), (c).end()
#define rev(a) reverse((a).begin(), (a).end())
#define each(x, a) for(auto& x : a)
#define mst(a, x) memset(a, x, sizeof(a))
#define rep(i, from, to) for(int i = from;i<to;i++)
#define rrep(i, from, to) for(i128 i = from;i>=to;i--)
#define to_uni(a) a.erase(unique(begin(a), end(a)), end(a))
#define fi first
#define se second
#define idx make_pair
#define pb push_back
#define endl "\n"
#define i128 __int128
#define ll long long
typedef pair<int, int> pii;
const int mod = 1e9 + 7;
const int dx[4]{1, 0, -1, 0}, dy[4]{0, 1, 0, -1};
const int fx[8] = {-1, -1, 0, 1, 1, 1, 0, -1}, fy[8] = {0, 1, 1, 1, 0, -1, -1, -1};
const int N = 1e5 + 10;
void solve() {
int n;
cin >> n;
vector<int> m(n);
ll sum = 0, count = 0;
each(x, m) {
cin >> x;
if (x < 0) count++, x = -x;
sum += x;
}
sort(all(m));
if (count % 2 == 1) sum -= 2 * m[0];
cout << sum << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}F. Range Update Point Query
Given an array $a1,a2,…,an$, you need to handle a total of $q$ updates and queries of two types:
- $1$ $l$ $r$ — for each index i with $l≤i≤r$, update the value of ai to the sum of the digits of ai.
- $2$ $x$ — output ax.
// F. Range Update Point Query
#include <bits/stdc++.h>
using namespace std;
#define all(c) (c).begin(), (c).end()
#define rev(a) reverse((a).begin(), (a).end())
#define each(x, a) for(auto& x : a)
#define mst(a, x) memset(a, x, sizeof(a))
#define rep(i, from, to) for(int i = from;i<to;i++)
#define rrep(i, from, to) for(i128 i = from;i>=to;i--)
#define to_uni(a) a.erase(unique(begin(a), end(a)), end(a))
#define fi first
#define se second
#define idx make_pair
#define pb push_back
#define endl "\n"
#define i128 __int128
#define ll long long
typedef pair<int, int> pii;
const int mod = 1e9 + 7;
const int dx[4]{1, 0, -1, 0}, dy[4]{0, 1, 0, -1};
const int fx[8] = {-1, -1, 0, 1, 1, 1, 0, -1}, fy[8] = {0, 1, 1, 1, 0, -1, -1, -1};
const int N = 2e5 + 10;
class BIT {
public:
vector<ll> tr;
int n;
BIT(int x) {
tr.resize(x + 1);
n = x;
}
void add(int x, int c) {
for (int i = x; i <= n; i += i & -i) tr[i] += c;
}
ll sum(int x) {
ll ans = 0;
for (int i = x; i; i -= i & -i) ans += tr[i];
return ans;
}
};
void solve() {
int n, q, op, l, r, idx;
cin >> n >> q;
BIT B = BIT(n);
vector<int> a(n + 1);
rep(i, 1, n + 1) cin >> a[i];
function<int(int)> calc = [&](int x) {
int ans = 0;
while (x) ans += x % 10, x /= 10;
return ans;
};
while (q--) {
cin >> op;
if (op == 1) {
cin >> l >> r;
B.add(l, 1);
B.add(r + 1, -1);
} else {
cin >> idx;
int num = a[idx];
for (int i = 0; i < min(3ll, B.sum(idx)); i++) num = calc(num);
cout << num << endl;
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}G1. Teleporters (Easy Version)
Consider the points $0,1,…,n$ on the number line. There is a teleporter located on each of the points $1,2,…,n$. At point $i$, you can do the following:
- Move left one unit: it costs 1 coin.
- Move right one unit: it costs 1 coin.
- Use a teleporter at point $i$, if it exists: it costs $ai$ coins. As a result, you teleport to point $0$. Once you use a teleporter, you can't use it again.
You have $c$ coins, and you start at point $0$. What's the most number of teleporters you can use?
// G1. Teleporters (Easy Version)
#include <bits/stdc++.h>
using namespace std;
#define all(c) (c).begin(), (c).end()
#define rev(a) reverse((a).begin(), (a).end())
#define each(x, a) for(auto& x : a)
#define mst(a, x) memset(a, x, sizeof(a))
#define rep(i, from, to) for(int i = from;i<to;i++)
#define rrep(i, from, to) for(i128 i = from;i>=to;i--)
#define to_uni(a) a.erase(unique(begin(a), end(a)), end(a))
#define fi first
#define se second
#define idx make_pair
#define pb push_back
#define endl "\n"
#define i128 __int128
#define ll long long
typedef pair<int, int> pii;
const int mod = 1e9 + 7;
const int dx[4]{1, 0, -1, 0}, dy[4]{0, 1, 0, -1};
const int fx[8] = {-1, -1, 0, 1, 1, 1, 0, -1}, fy[8] = {0, 1, 1, 1, 0, -1, -1, -1};
const int N = 2e5 + 10;
void solve() {
int n, c, ans = 0;
cin >> n >> c;
priority_queue<int> q;
for (int i = 1, x; i <= n; ++i) {
cin >> x;
q.push(-x - i);
}
while (!q.empty()) {
int x = -q.top();
q.pop();
if (x > c) break;
++ans;
c -= x;
}
cout << ans << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}








Comments | 2 条评论