西藏加油~
矩阵中的局部最大值
给你一个大小为 n x n 的整数矩阵 grid 。
生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ,并满足:
maxLocal[i][j]等于grid中以i + 1行和j + 1列为中心的3 x 3矩阵中的 最大值 。
换句话说,我们希望找出 grid 中每个 3 x 3 矩阵中的最大值。
返回生成的矩阵。
示例 1:
输入:grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
输出:[[9,9],[8,6]]
解释:原矩阵和生成的矩阵如上图所示。
注意,生成的矩阵中,每个值都对应 grid 中一个相接的 3 x 3 矩阵的最大值。示例 2:
输入:grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
输出:[[2,2,2],[2,2,2],[2,2,2]]
解释:注意,2 包含在 grid 中每个 3 x 3 的矩阵中。提示:
n == grid.length == grid[i].length
3 <= n <= 100
1 <= grid[i][j] <= 100实质呢就是一个3*3的卷积核,然后进行最大卷积。
这样的话进行一个模拟就可以了。
数据很小,时间复杂度$O(9n^2)$可以过
class Solution {
public:
vector<vector<int>> largestLocal(vector<vector<int>> &grid) {
vector<vector<int>> ans(grid.size() - 2, vector<int>(grid.size()-2, 0));
int n = grid.size();
for (int i = 0; i < n - 2; i++) {
for (int j = 0; j < n - 2; j++) {
int cnt = grid[i][j];
for (int k = i; k < i + 3; k++) {
for (int m = j; m < j + 3; m++) {
cnt = max(cnt, grid[k][m]);
}
}
ans[i][j] = cnt;
}
}
return ans;
}
};边积分最高的节点
给你一个有向图,图中有 n 个节点,节点编号从 0 到 n - 1 ,其中每个节点都 恰有一条 出边。
图由一个下标从 0 开始、长度为 n 的整数数组 edges 表示,其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的 有向 边。
节点 i 的 边积分 定义为:所有存在一条指向节点 i 的边的节点的 编号 总和。
返回 边积分 最高的节点。如果多个节点的 边积分 相同,返回编号 最小 的那个。
示例 1:
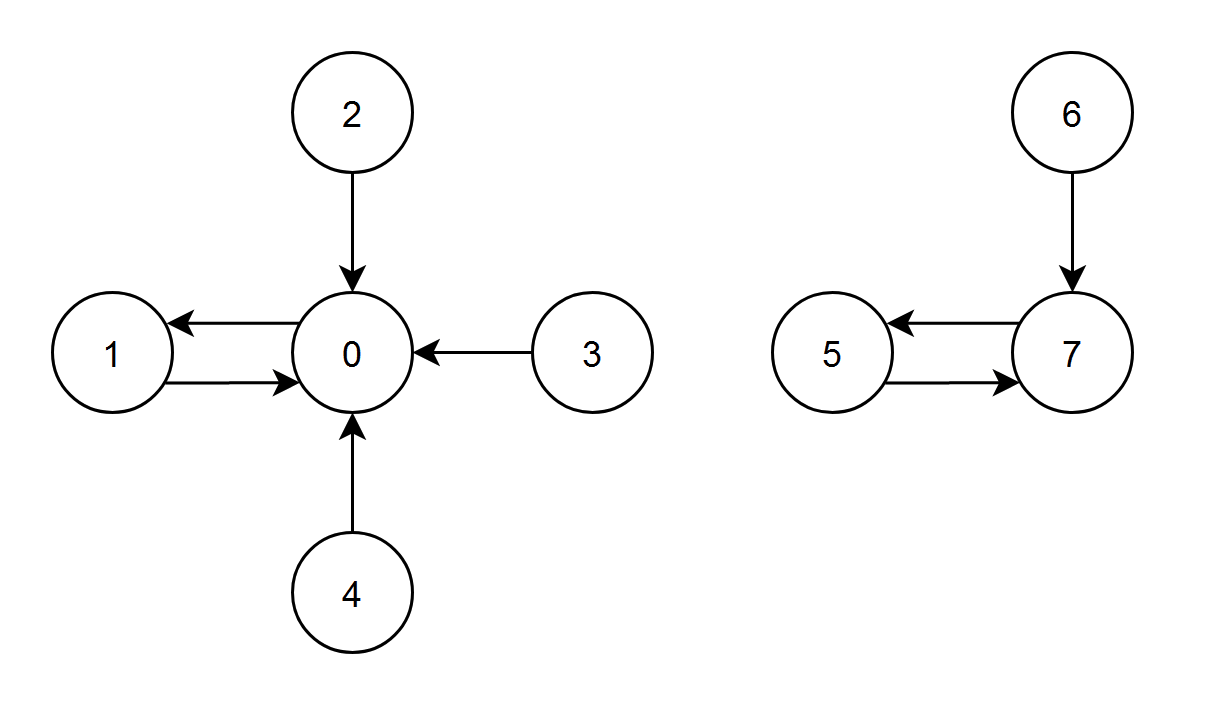
输入:edges = [1,0,0,0,0,7,7,5]
输出:7
解释:
- 节点 1、2、3 和 4 都有指向节点 0 的边,节点 0 的边积分等于 1 + 2 + 3 + 4 = 10 。
- 节点 0 有一条指向节点 1 的边,节点 1 的边积分等于 0 。
- 节点 7 有一条指向节点 5 的边,节点 5 的边积分等于 7 。
- 节点 5 和 6 都有指向节点 7 的边,节点 7 的边积分等于 5 + 6 = 11 。
节点 7 的边积分最高,所以返回 7 。示例 2:
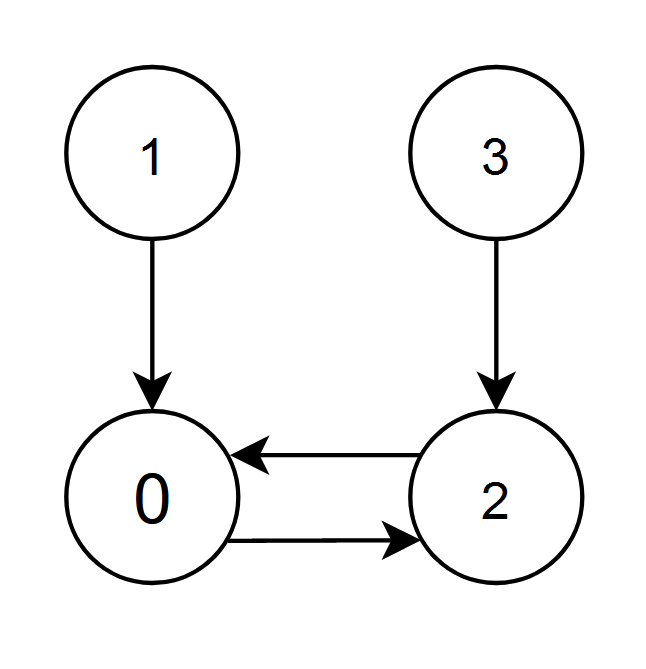
输入:edges = [2,0,0,2]
输出:0
解释:
- 节点 1 和 2 都有指向节点 0 的边,节点 0 的边积分等于 1 + 2 = 3 。
- 节点 0 和 3 都有指向节点 2 的边,节点 2 的边积分等于 0 + 3 = 3 。
节点 0 和 2 的边积分都是 3 。由于节点 0 的编号更小,返回 0 。提示:
n == edges.length2 <= n <= 1050 <= edges[i] < nedges[i] != i
这个题就跟图没啥关系吧,
直接开一个数组从头到尾算一遍看看哪个点为入度的节点序号和最大
然后几行代码就出来了。真的很简单!数组题不是图题
时间复杂度$$O(n)$$
空间复杂度$$O(n)$$
class Solution {
public:
int edgeScore(vector<int> &edges) {
vector<long long> ans(edges.size(), 0);
for (int i = 0; i < edges.size(); i++) {
ans[edges[i]] += i;
}
return max_element(ans.begin(), ans.end()) - ans.begin();
}
}; 根据模式串构造最小数字
给你下标从 0 开始、长度为 n 的字符串 pattern ,它包含两种字符,'I' 表示 上升 ,'D' 表示 下降 。
你需要构造一个下标从 0 开始长度为 n + 1 的字符串,且它要满足以下条件:
num包含数字'1'到'9',其中每个数字 至多 使用一次。- 如果
pattern[i] == 'I',那么num[i] < num[i + 1]。 - 如果
pattern[i] == 'D',那么num[i] > num[i + 1]。
请你返回满足上述条件字典序 最小 的字符串 num。
示例 1:
输入:pattern = "IIIDIDDD"
输出:"123549876"
解释:
下标 0 ,1 ,2 和 4 处,我们需要使 num[i] < num[i+1] 。
下标 3 ,5 ,6 和 7 处,我们需要使 num[i] > num[i+1] 。
一些可能的 num 的值为 "245639871" ,"135749862" 和 "123849765" 。
"123549876" 是满足条件最小的数字。
注意,"123414321" 不是可行解因为数字 '1' 使用次数超过 1 次。示例 2:
输入:pattern = "DDD"
输出:"4321"
解释:
一些可能的 num 的值为 "9876" ,"7321" 和 "8742" 。
"4321" 是满足条件最小的数字。提示:
1 <= pattern.length <= 8pattern只包含字符'I'和'D'。
(1)首先很容易证明,如果让结果更小,首先应该是从1-len的组成的,不可能有更大的数出现。
(2)最大的数越晚出现越好,这样的话就可以进行贪心处理。
(3)如果当前位置出现的DI的情况,那么可以证明xy变为yx是最小的,
(4)因此只需要找每个子串D……I,然后将这一部分转换位置就可以了
时间复杂度$$O(n)$$
空间复杂度$$O(1)$$
class Solution {
public:
string smallestNumber(string p) {
string ans;
for (char ch = '1'; ch <= '1' + p.size(); ch++) {
ans += ch;
}
for (int i = 0; i < p.size(); i++) {
if (p[i] == 'D') {
int j = i;
while (p[j] == 'D') {
j++;
}
reverse(ans.begin() + i, ans.begin() + j + 1);
i = j;
}
}
return ans;
}
};统计特殊整数
如果一个正整数每一个数位都是 互不相同 的,我们称它是 特殊整数 。
给你一个 正 整数 n ,请你返回区间 [1, n] 之间特殊整数的数目。
示例 1:
输入:n = 20
输出:19
解释:1 到 20 之间所有整数除了 11 以外都是特殊整数。所以总共有 19 个特殊整数。示例 2:
输入:n = 5
输出:5
解释:1 到 5 所有整数都是特殊整数。示例 3:
输入:n = 135
输出:110
解释:从 1 到 135 总共有 110 个整数是特殊整数。
不特殊的部分数字为:22 ,114 和 131 。提示:
1 <= n <= 2 * 10^9
很明显呢,是需要进行数位DP的
数位dp,从数的高位到低位进行递推
// index表示数的第几位,最低位为0
// repeated表示index位前面的数中是否出现了重复数字
// cling index位前面的数是否紧贴上限,如n=5736 , 取十位数时,如果千位和百位分别为5和7,表示紧贴,十位的选择只能是[0,3];非紧贴取数范围为[0,9]
// nonLeadingZeroCount 非前导零个数 0034为2 0010为2
dfs(int index, boolean repeated, boolean cling, int nonLeadingZeroCount)
class Solution {
public:
int frac[11];
int nnum[10];
bool flag[10];
int A(int m, int n) {
if (n > m)return 0;
if (m == 0)return 0;
return frac[m] / frac[m - n];
}
int sum(int total, int curr) {
if (curr < 0)return 1;
int result = 0;
int n = nnum[curr];
for (int i = n - 1; i >= 0; i--) {
if (total == curr + 1 && i == 0) {
for (int j = curr; j > 0; j--) {
result += (A(10, j) - A(9, j - 1));
}
} else if (!flag[i])result += A(10 - total + curr, curr);
}
if (!flag[n]) {
flag[n] = true;
result += sum(total, curr - 1);
}
return result;
}
int countSpecialNumbers(int n) {
frac[0] = frac[1] = 1;
for (int i = 2; i < 11; i++)frac[i] = frac[i - 1] * i;
memset(nnum, 0, sizeof(nnum));
memset(flag, 0, sizeof(flag));
int N = n;
int d = 0;
while (N) {
nnum[d++] = N % 10;
N /= 10;
}
return sum(d, d - 1);
}
};








Comments | NOTHING